【化学基礎】原子量計算の裏技!をわかりやすく解説!定期テスト対策に!
原子量ってそもそも何?
さて、それでは化学基礎において、一番最初の計算分野でもある「原子量計算」をやっていきたいと思います。
原子量計算・・を行う前に、そもそも原子量ってなんですか?
死ぬほど分かりにくいですよね、原子量・・・。
実はわかりにくいのは皆さんのせいではなく・・・この物語が
「相対質量」→「原子量」→「物質量」という3本建てになっているからなのです!!!
相対質量・・・とは??
例えば私の年齢を32歳とします。
あなたの年齢を16歳とします。
例えば私の年齢(32歳)を1とします。
するとあなたの年齢は0.5になります。(半分なので)
最初の32歳・16歳が実際の年齢(絶対年齢)だとすると、
後半の1と0.5は相対年齢という仮の数値になります。
これが「相対」(相手と比較してどうか)という意味なのですが・・
いや、32歳と16歳でええやん!って思いましたよね?
そう、そうなのです。
ただし
人間の扱える数字の範囲であれば・・・・です。

これ、原子1個の重さなのですが・・・
どうですか?すごく嫌じゃないです??
マイナス24乗っていうのは、0.000000000000000000000000…ってことです。
あまりにも計算がしにくい。
そこで人類が生み出した苦肉の策が相対質量なのです。

そもそも、各原子には質量数と呼ばれる、明らかに質量に関連しそうな数値が存在します。まあ、これを使おうと思ったわけですね。
で、まあ、探すんですよ。ちょうどいいのを。
当然最初は「質量数1の水素原子の質量を1とすると・・」とかしてたのですが、そうすると他の原子の相対質量が質量数とずれてしまう。
質量数がそのまま相対質量になる、みたいな都合のいいやつ居てくれ~!
って探したわけです。
いました。質量数12の炭素原子です。
こやつを基準に相対質量を決めると、なんともまあ、質量数とほぼ同じになるわけで。
こりゃあいいな!と決めたわけです。
これで計算が少し楽になるな・・と思いきや、人類は次の問題にぶち当たります。
同じ元素記号なのに質量数違うやついるんだが・・・
そう、同位体(同じ元素記号の原子でも質量数が異なるもの同士)です。
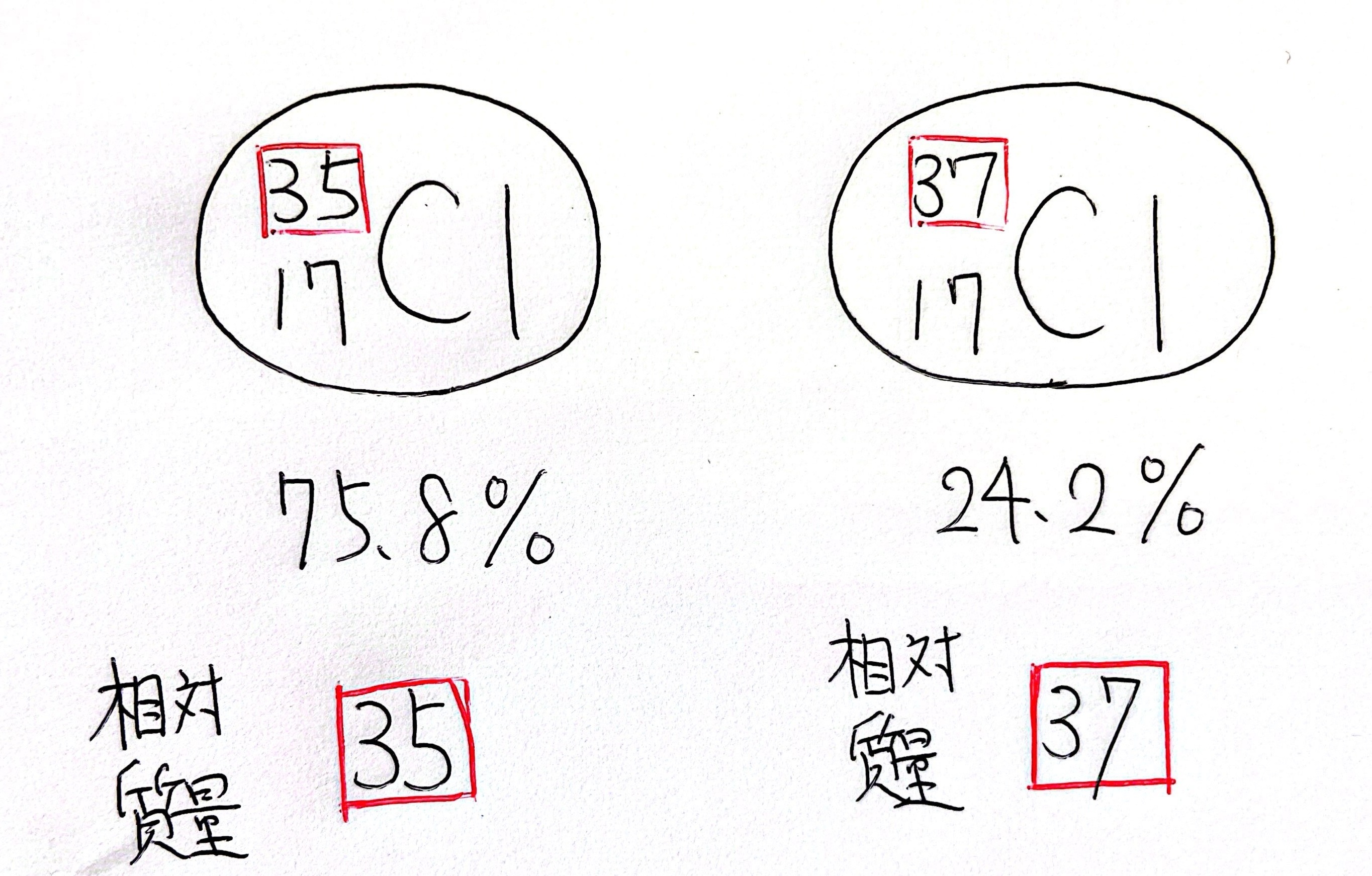
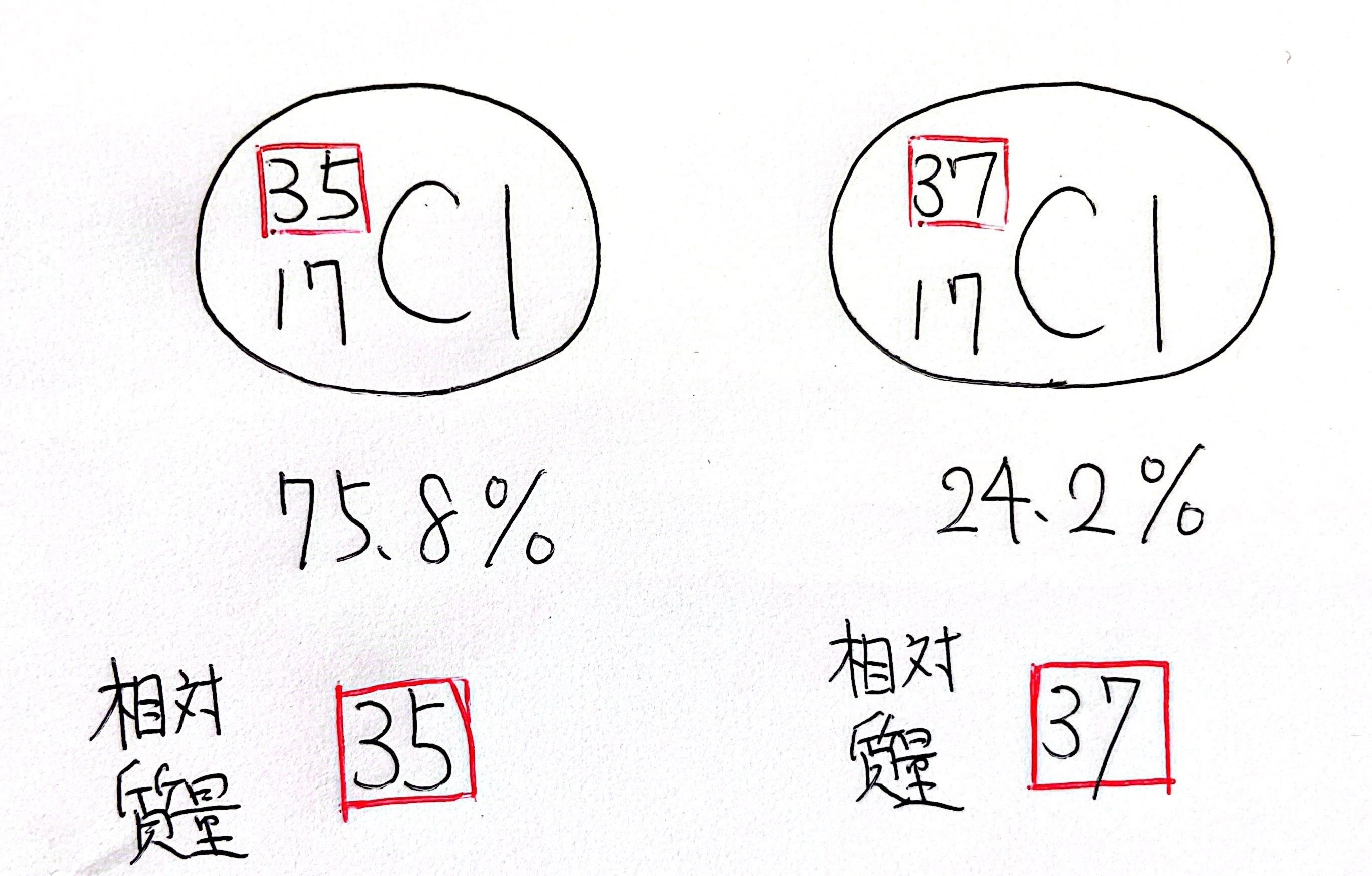
こんな感じで、塩素Cl原子にも質量数35のやつと37のやつがいます。
まあ原子にも体重には差があって、重いやつと軽いやつがいると。
ただ、この質量数と相対質量を一致させているので、塩素を考えるときはどっちにすればいいの?!ってなります。
ということで、平均をとってしまおうと。
この平均を取った相対質量のことを原子量といいます。
立式はまあ簡単ではあるけども・・?
簡単とか書いてますが、平均というものにも少しだけ気を付けなければならないところがありまして。
例えば私の試験が「100点」と「0点」しかいなかったとします。
どんな試験だよっていう感じですが、たぶん配点100の問題が1個だけとかにすればこういう感じになりますね。
すると平均は・・・100と0だから50!!!となるかというとわからんわけです。
例えば40人の学級で、「39人が100点」、「1人が0点」だったとします。
これ、学級の平均点って50だと思います?
・・・たぶん違いますよね。
ほとんどの人が100点だから、平均点も100点に近づきますよね?
これ、原子1個の重さなのですが・・・
どうですか?すごく嫌じゃないです??
マイナス24乗っていうのは、0.000000000000000000000000…ってことです。
あまりにも計算がしにくい。
そこで人類が生み出した苦肉の策が相対質量なのです。

そもそも、各原子には質量数と呼ばれる、明らかに質量に関連しそうな数値が存在します。まあ、これを使おうと思ったわけですね。
で、まあ、探すんですよ。ちょうどいいのを。
当然最初は「質量数1の水素原子の質量を1とすると・・」とかしてたのですが、そうすると他の原子の相対質量が質量数とずれてしまう。
質量数がそのまま相対質量になる、みたいな都合のいいやつ居てくれ~!
って探したわけです。
いました。質量数12の炭素原子です。
こやつを基準に相対質量を決めると、なんともまあ、質量数とほぼ同じになるわけで。
こりゃあいいな!と決めたわけです。
これで計算が少し楽になるな・・と思いきや、人類は次の問題にぶち当たります。
同じ元素記号なのに質量数違うやついるんだが・・・
そう、同位体(同じ元素記号の原子でも質量数が異なるもの同士)です。

こんな感じで、塩素Cl原子にも質量数35のやつと37のやつがいます。
まあ原子にも体重には差があって、重いやつと軽いやつがいると。
ただ、この質量数と相対質量を一致させているので、塩素を考えるときはどっちにすればいいの?!ってなります。
ということで、平均をとってしまおうと。
この平均を取った相対質量のことを原子量といいます。
立式はまあ簡単ではあるけども・・?
簡単とか書いてますが、平均というものにも少しだけ気を付けなければならないところがありまして。
例えば私の試験が「100点」と「0点」しかいなかったとします。
どんな試験だよっていう感じですが、たぶん配点100の問題が1個だけとかにすればこういう感じになりますね。
すると平均は・・・100と0だから50!!!となるかというとわからんわけです。
例えば40人の学級で、「39人が100点」、「1人が0点」だったとします。
これ、学級の平均点って50だと思います?
・・・たぶん違いますよね。
ほとんどの人が100点だから、平均点も100点に近づきますよね?

この図にあるように、質量数35の塩素は75.8%存在していて、質量数37の塩素は24.2%存在しています。
ここを考慮しなければならない!
でも大丈夫!それさえ知っていたら立式は簡単!!!!

どうです?意外と直感と合っている立式のはずです。
よしよし、出来ました。さあ、あとは計算するだけです。
計算するだけですが・・・どうですか?
私はこれを暗算できますが、あなたはどうですか?
では、奥義を伝授します。
最強奥義!原子量計算はこれでイチコロ・イチココミロ

まず、37を(35+2)にします。
なんで!?という感じだと思いますが、まあまあ、最後まで見て行ってください。
なお、ここからの操作はわりとテクニカルな数式処理になりますが、ひとつひとつは中学校1年生レベルの話なので、あまり怖がらずに見ていきましょう。
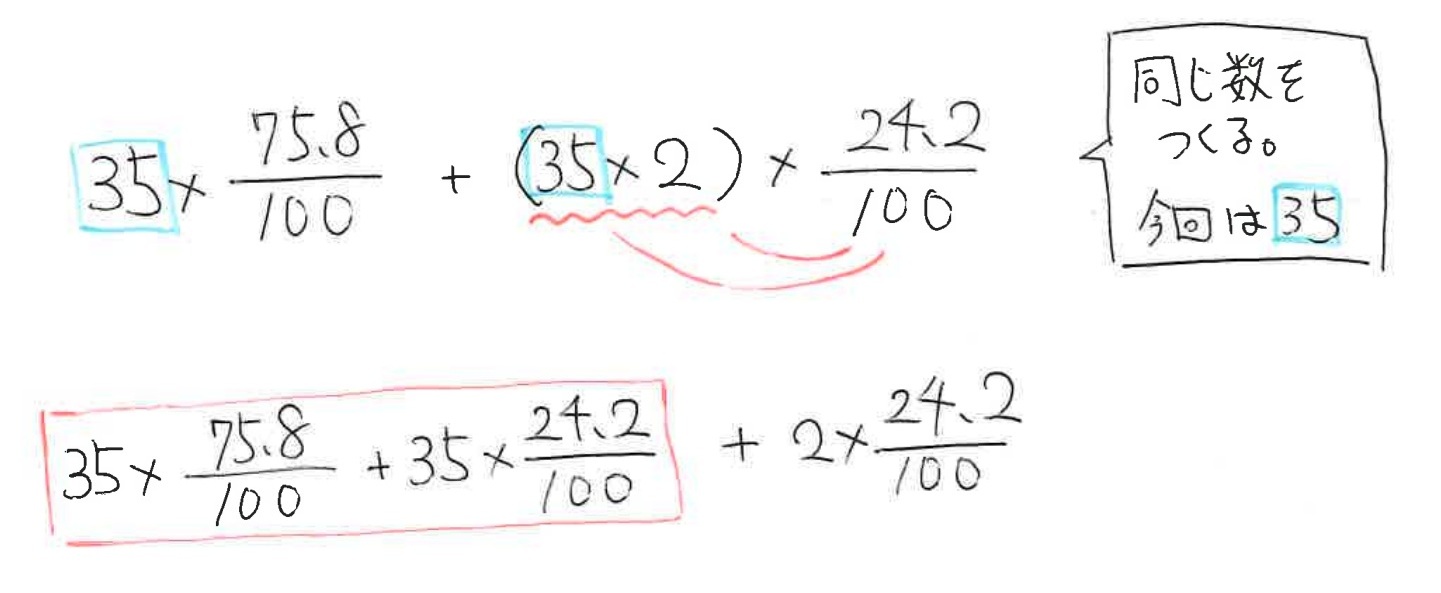
次に、(35+2)としているので、分配法則が働きますので、展開します。
すると、赤い四角で囲っているところに共通な数字(共通因数)である35が生まれるので、今度はここをまとめます。(因数35を用いて因数分解する、ということです)

すると、ここでなんと!100/100 = 1となる部分が出てきます。
よって、最初に作った35という数字はそのまま残り、
必要な計算はわずかに残った部分だけになります!
この手法は、パーセンテージが全て足すと100%(割合が1)のときに使用できる普遍的な方法です。
化学ではここ以外で使用する機会は無いですが、物理や生物、それこそ数学などでは使用できることがあるかもしれません。
なお、今回は35と37を、35を残す目的で「35と(35+2)」にしましたが、
37を残す目的で「(37-2)と37」にしても同じように計算できます。
ぜひ試してみてください。この場合は37が残ります。
大切なポイントは自分が残した数字がそのまま出てくる、ということです。
以上!原子量計算の奥義でした!
なお、今後の主な舞台はnote(<無料公開>【化学基礎】原子量計算の奥義!最強の裏技をわかりやすく解説!高校生にも教員にも。|ココミロ)になる可能性が高いです。
面白かった、役に立った、次も読みたい!という場合はnoteにスキとフォローをお願いします!
読者からの反応が一番のエネルギー源です。
なお、Xアカウントもあります。貼っておくのでこちらもフォローお願いします。
見たらわかるように作り立てホヤホヤ。
今からフォローしたら古参になれます。
ココミロかんりにん(@kokomiroseibutu)さん / X




