【生物基礎】DNAの全長計算問題の解き方を解説

【問題】

DNAの二重らせんは10塩基対ごとに１周する。

１周のらせんの長さは3.4nm（ナノメートル）だった。

ヒト細胞の核１個のDNA量が5.9pg（ピコグラム）とすると、

DNAの全長は何mになるか答えよ。

ただし、１gのDNAには１.0×10^21（10の21乗）塩基対が含まれ、

１nmは10^9分の１（10の1/9乗）m、1pgは10^12分の1（10の1/12乗）gとする。

解答の発想

この手の計算問題が苦手な受験生は多い。

だが、センター試験には必ず計算問題が出るし（むしろ次はこれじゃないかという気さえする）、

二次試験でも計算問題は出る。差がつく場所なので、良い差をつける側になろう。

さて、問題を見たときに、何をしていいかわからなくなる場合がある。

その時は何を聞かれているかを見るのだ。

今回、「DNAの全長が何ｍなのか」が聞かれている。「長さ」だ。

だから我々は、「長さ」について記述されているところをまず探す。

条件の整理

長さの情報には「らせんの情報」が混ざっていた。

したがって、次は「らせんの情報」を探す。

そして「長さの情報」と「らせんの情報」を合わせると、「１０塩基対で３．４nmである」という条件が浮かび上がる。

我々はいま、長さを出したいのだが、塩基対の数がわかれば長さがわかるという見通しがたった。

次に考えるのは、当然、「DNAの塩基対の数」だ。これがわかれば「長さ」がわかるのだから。

すると、「１ｇのDNAに含まれる塩基対の数」の情報があり、「核の重さ」の情報がある。

これを「比の形」で立式する。同じDNAを用いているのだから、重さと塩基対の数の関係性は変わらないことを背景に用いている。

ただし、注意点として、「単位をそろえる」必要がある。「g」と「pg」が混在していてはダメなので、「g」に合わせる。

この比の形を立式できたとき、「＝の内側同士」と「＝の外側同士」を掛け合わせたものが等しくなる、という関係がある。これを用いる。

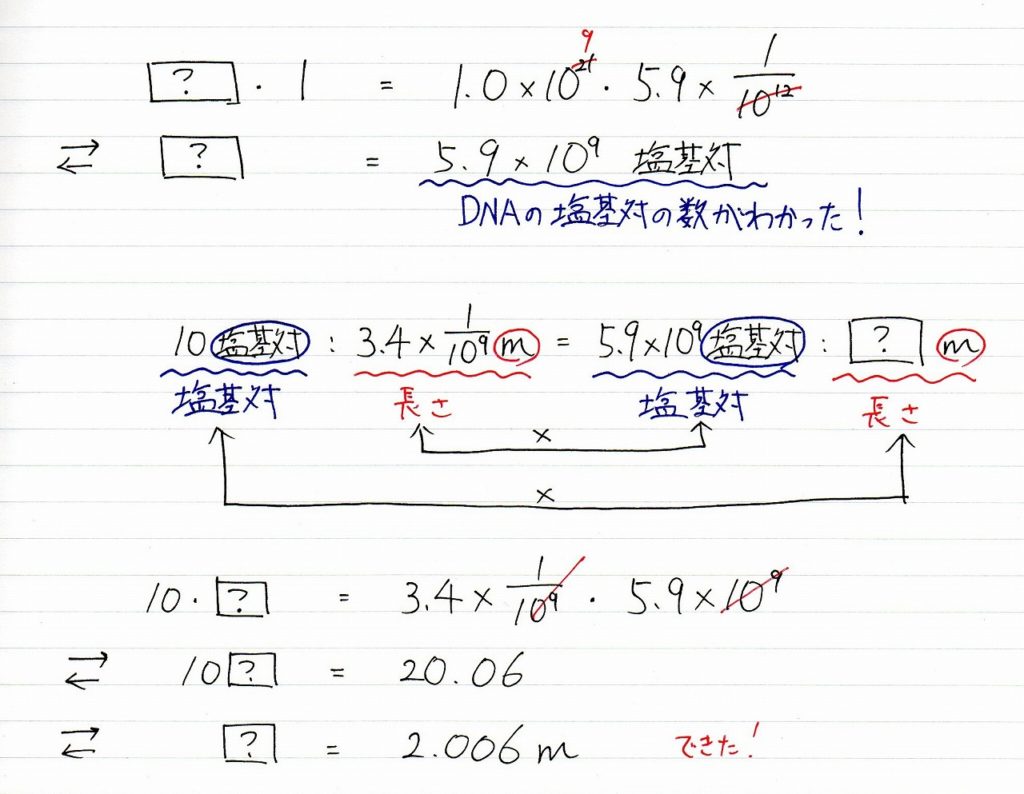
すると、DNAの塩基対の数がわかる。

「１０塩基対で３．４nm」であり、「５．９×10^9塩基対」あることがわかったのだから、また比の形で立式できる。

「単位」に注意し、「nm」を「m」にそろえる。

＝の内側と外側の関係性により、DNAの全長が2.006mだということがわかった。

この結果は衝撃的でもある。

あなたの細胞１個の核に含まれるDNAの全長は2mもあるのだ。

逆にいうと、DNAは核の中には折りたたまれて入っていることも予想できる。
（これに関してはこちらの投稿も合わせてご確認ください）

以上。

計算問題に限らず、解法が思いつかない場合は、

「そもそも何を聞かれているのか？」に立ち戻ってみること。